Variabilidad de traslación
Este trabajo es una extracción de la tesis que se pressenta como referencia.
Terminología
Un genotipo es una cadena de tamaño finita sobre un alfabeto finito.
El término cromosoma y genotipo son equivalentes.
Fenotipo -phenotype-
Un fenotipo es una solución potencial del problema de optimización que se esté atacando.
Un fenotipo es codificado dentro de un genotipo mediante alguna codificación dependiente del problema o una función de mapeo.
Los elementos del alfabeto son llamados bases, una base específica en una posición específica en el cromosoma es conocido como allele.
La combinación de genotipo, alfabeto y función de aptitud es conocida
como individuo.
Esquemas de selección
En Algoritmos Genéticos -AG- la selección implementa el principio natural de la supervivencia del mas apto.
En la selección, se escogen aleatoriamente los individuos que serán insertados a la piscina o depósito de apareamiento para ser recombinados.
La selección está influenciada por la aptitud de los individuos.
Los individuos con un valor alto en su función de aptitud serán insertados en el depósito mas frecuentemente que aquellos con función de aptitud inferiores.
La selección en AG consiste básicamente de dos pasos:
Se calculan las probabilidades de selección pi � R0+ para todos los individuos de la población actual, por lo tanto
�i = 1npi = 1
El rango de descendencia esperado de un individuo es ei = N·pi, por lo tanto, las probabilidades de selección son calculadas explícitamente
Se extraen N individuos -con reemplazo- de la población actual y se insertan copias de estos en el depósito de apareamiento. El proceso está determinado por las probabilidades de selección y es llevado a cabo por algún algoritmo de muestreo.
La diferencia entre el número de copias con que contribuye un individuo al depósito y el número de descendientes ei esperado determina la precisión del esquema de muestreo.
Cabe hacer notar que existen esquemas de selección que realizan ambos de los pasos descritos en uno solo.
Selección dinámica y estática
Los esquemas de selección que no requieren los valores absolutos del valor de aptitud para calcular la probabilidad de selección son conocidos como estáticos. Por ejemplo, ya que en el proceso de Selección por Rango solo se compara la aptitud entre individuos, las probabilidades de selección permancen constantes para todas las generaciones.
Los métodos como Selección Proporcional son llamados dinámicos porque la aptitud absoluta es necesaria en el cálculo de las probabilidades de selección. Por consiguiente, es necesario calcular estas probabilidaes en cada generación.
Dado que las probabilidades dependen explícitamente de la distribución de aptitud de la población, entonces son dinámicas.
Aunque no existe una definición formal del término, éste se refiere al subconjunto de parámetros de AG que influyen en la frecuencia de selección de los individuos de acuerdo a su aptitud.
Una presión de selección baja indica que el AG selecciona a la mayoría de los individuos independientemente de su valor de aptitud. Por el contrario, un AG tiene una presión de selección alta si solo son insertados al depósito los individuos mas aptos, y como consecuencia, solo estos pueden transmitir sus genes a las generaciones sucesivas.
Una presión de selección baja pone mayor énfasis en la exploración del espacio de búsqueda que en la explotación, dado que la mayoría de los individuos transmiten su información genética.
Una presión de selección alta resulta en una explotación, dado que solo los individuos mejores contribuyen con su material genético para la reproducción, i.e. el proceso de búsqueda es enfocado a regiones específicas para identificar soluciones -sub- óptimas.
Por lo anterior, la presión de selección afecta la diversidad genética.
Extinctividad
Un método de seleccioón es extinctivo si individuos en particular, especialmente los de menor aptitud son excluidos en la reproducción con probabilidad de selección pi = 0.
Algoritmos de muestreo
Se asigna una parte -rebanada- de tamaño pi de la rueda de la ruleta a cada individuo, se gira N veces la ruleta y se insertan en el depósito los N individuos ganadores.
Se inserta un número de individuos igual a la parte entera del porcentaje de descendencia esperada ei al depósito.
La parte restante es muestreada con el método de la ruleta hasta que se llena el depósito.
Es una variante mejorada del método de la ruleta, esto es, se ponen N marcadores espaciados de manera uniforme en la ruleta, por lo tanto, la rueda solo se gira una vez. Mientras la complejidad del primero es O(n2), la del último es de O(n).
Un error de muestreo pequeño reduce la desviación o tendencia genética, la cual lleva a la población a converger debido a los errores de muestreo acumulados. Esto es, la diferencia entre la frecuencia actual de muestreo y la probabilidad de selección calculada causará eventualmente que ciertos alleles se desvanezcan de la población.
El desvanecimiento de alleles debido a los errores de muestreo causan que el AG converja a mínimos locales, obsérvese que la mutación resuelve parcialmente este problema.
La desviación se define como la diferencia absoluta entre la probabilidad actual de muestreo de un individuo y su valor esperado.
Cada individuo puede recibir un cierto número de copias insertadas en el depósito de apareamiento durante la fase de muestreo.
El rango posible del número de copias es llamado propagación -o dispersión-.
SUS garantiza una dispersión mínima y desviación cero
Selección Aleatoria
No es muy práctica, sin embargo se describe para simular el comportamiento de algoritmos de búsqueda aleatoria. Tal simulación no es perfecta dado que la selección arbitraria de individuos es restringida a ciertos alcances debido a los operadores de cruza y mutación. Esta técnica selecciona individuos a reproducir mediante el muestreo uniforme con reemplazo de la población.
pi = 1/N,i � {1,...,N}
Las probabilides de selección para los individuos está determinada por:
pi = [(fi)/( �s = 1nfs)],i � {1,...,N}|�s = 1npi = 1
La aptitud fi de las cromosomas es dividida por la suma de todos los valores de aptitud. Aunque este método puede implementarse de una manera sencilla, tiene problemas de escalamiento.
Esto es, PS no es invariante a la traslación.
Un ejemplo de variabilidad de traslación es el siguiente:
Considérese una población con dos individuos
Aptitud del individuo 1 f1 = r, r � R0+
Aptitud del individuo 2 f2 = r+1, r � R0+
Entonces las probabilidades calculadas serán:
p1 = [r/( 2r+1)]
p2 = [(r+1)/( 2r+1)]
Nótese que la diferencia en aptitud es constante para ambos individuos, pero las probabilidades de selección p1 pueden cambiar arbitrariamente con r en el rango [0,1/2) y p2 en el rango (1/2,1].
Otro problema de escalamiento es causado por la distribución de los valores de aptitud. Por ejemplo, si hay un individuo con aptitud excepcional en la población al inicio, entonces este individuo será seleccionado la mayoría de las veces, lo que puede causar que el AG converja a un óptimo local, i.e. convergencia prematura.
Se selecciona el individuo con la peor aptitud de las últimas w poblaciones como una línea base fbase = fpeor. w es el tamaño de la ventana y determina el número de generaciones a monitorear para las funciones de aptitud peores.
Los valores típicos -enteros- para w son 1-10. Después de esto, todos los otros valores de aptitud de la población son ajustados a la línea base. En realidad, el peor valor de aptitud es eliminado de los otros valores de aptitud
fi� = fi-fbase,i � {1,...,N}
Este proceso de normalización elimina la deficiencia en la variabilidad de traslación de PS.
Un problema con este método es, si la población actual contiene un individuo con muy baja aptitud, entonces fallará. Este problema se presenta por que no existe garantía de que los nuevos cromosomas creados tengan mejor aptitud que sus ancestros.
Se introduce una línea base para ajustar la aptitud de una población para tratar el problema con los valores de aptitud muy bajos.
Primero: Se calcula la media [`f] = 1/N�i = 1Nfi y la desviación estándard sdf = �{[1/( N-1)]�i = 1N(fi-mf)2} de la aptitud de la población.
Segundo: La línea base fbase es la desviación estándard escalada con algún valor apropiado g � (R) restado de la media fbase = [`f]-g·sdf. El escalonamiento provee de una ''manija'' para ajustar la presión de selección.
Después, las probabilidades de selección son derivadas de los valores de aptitud alteradas.
No se debe perder de vista que esta técnica puede introducir valores de aptitud negativos, los cuales por definición son inválidos. Este problema puede ser resuelto haciendo estos valores a cero.
Escalamiento lineal previene que los individuos con valores grandes de aptitud se reporduzcan muy rápidamente para evitar una convergencia prematura.
Los individuos mas aptos reciben una probabilidad de selección de pmejor = 1/Ns
Los individuos con aptitud promedio reciben una probabilidad de selección de pavg = 1/N
Se supone que pi = 1/N(1+[(fi+f)/( fmejor-[`f])](s-1)),i � {1,...,N}
El factor de escalamiento s está en el rango [1,2]. Si s es puesto como s = 1+[(fmejor+f)/([`f]-fpeor)] no ocurrirán probabilidades de selección negativas, esto es, el peor individuo tendrá una probabilidad de cero. Por el contrario, si s es puesto en un valor arbitrario entre 1 y 2, entonces podrán ocurrir probabilidades de selección negativas.
La idea básica de BWS es tomada del algoritmo de recocido simulado. En la primera, se introduce un parámetro de tolerancia T, el cual es comparable con la temperatura del recocido simulado. Para valores grandes de T la tolerancia es alta, esto significa que la presión de selección es relativamente baja, pero al decrementar T durante la corrida del AG la presión de selección se va equilibrando, pi está definido de la manera siguiente:
pi = [(e[(fi)/ T])/( �s = 1Ne[(fs)/ T])],i � {1,...,N}
En BWS no se necesitan transformaciones de la función objetivo para obtener solo valo
res de aptitud positivos.
BWS es invariante a la translación y al escalamiento.
No es claro como obtener el valor ''óptimo'' de T, dado que esto parece ser dependiente del problema.
Estos métodos intentan resolver los problemas relacionados con la variabilidad de traslación. Para ello, la probabilidad de selección no se deriva de la aptitud de un individuo, en vez de ello es derivada de su rango. Primero son ordenados los individuos con respecto a su aptitud, enseguida se les asigna su probabilidad de acuerdo al rango que ocupan en la población.
N es el tamaño de la población y al mismo tiempo el rango mas alto. La población es ordenada con respecto a la aptitud individual. El rango más alto es asignado al individuo con más alto valor de aptitud y el rango más bajo al individuo con el valor de aptitud más bajo. Aún en el caso de que existan individuos con igual aptitud, tendrán diferentes rangos; por lo tanto habrá N individuos con N diferentes rangos.
Las probabilidades de selección son asignadas de acuerdo al rango de los individuos
pi = 1/N(h++(h+-h-)[(N-i)/( N-1)]),i � {1,...,N}
La función lineal convierte los rangos en probabilidades de selección.
La condición �i = 1npi = 1 requiere 0 � h- � 1 y h+ = 2-h-. Como consecuencia, el individuo mas apto será seleccionado con probabilidad [(h+)/ N] y el peor con [(h-)/ N]
Una afinación del esquema anterior transforma una variable aleatoria c � \lbrack0,1] uniformemente distribuida para deteminar el índice del individuo a seleccionar i = �[N/( 2(c-1))](c-�{c2-4(c-1)c})�
Donde el parámetro c � (1,2] determina que los individuos con mejor aptitud sean muestreados con una frecuencia alta.
Ambas técnicas son idénticas para c = h+.
Este método genera una presión de selección con rango medio bajo, debido a la distribución lineal de las probabilidades de selección.
Las probabilidades de selección son pesadas exponencialmente de acuerdo a la siguiente fórmula:
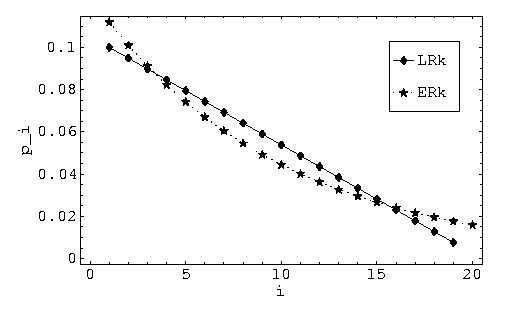
pi = [(ci-1)/( �i = 1NcN-1)]( � [(c-1)/( cN-1)]ci-1),i � {1,...,N}
Comparado con LRk, este método asigna probabilidades mas altas a los individuos con mayor y menor aptitud, pero asigna probabilidades mas bajas a individuos con aptitud media.
Es por esto que ERk preserva la diversidad en la población. Además, se puede obtener una presión de selección mas alta con LRk porque las probabilidades pueden ser distribuidas en una forma mas flexible.
En lugar de asignar probabilidades a cada individuo, se organiza a éstos aleatoriamente en grupos de tamaño fijo. Los individuos mas aptos de un grupo i.e. los ganadores del torneo son insertados al depósito de apareamiento. El procedimiento se repite hasta que se llena el depósito.
El número de individuos en un grupo tiene un impacto substancial en la presión de selección. Generalmente, grupos grandes reducen drásticamente la oprtunidad de los indivuduos con aptitud media o baja de ser copiados en el depósito. En consecuencia, la presión de selección se incrementa con grupos grandes.
El tamaño del torneo es t � N, donde valores grandes de torneo, i.e. t � 2 intensifican la competencia entre individuos y por consiguiente incrementan la presión de selección del AG.
Los torneos son de tamaño t pero se utilizan lanzamientos de una moneda cargada para determinar si el individuo mas apto o un individuo arbitrario del grupo del torneo es insertado en el depósito, esto se hace para decrementar la persión de selección. El individuo mas apto gana el torneo con una probabilidad p, tal que 0.5 < p < 1. p permanece constante durante una corrida. Al decrementar p, la presión se va estabilizando -hacia abajo-.
Además de t, p provee otro parámetro para ajustar la presión de selección de TS.
Para cada lugar del depósito se tiene un torneo ternario (t = 3). Donde el primer individuo I1 es seleccionado aleatoriamente, después, I2 e I3 son seleccionados aleatoriamente pero tienen que ser diferentes en aptitud con respecto a I1 en un valor Q dado. Con una oportunidad de 50%, I3 también deberá diferir de I2 en Q. Se asume que todos los individuos pertenecen a clases de diferente valor de aptitud. Q debe ser lo suficientemente pequeña tal que todas las clases sean distinguidas.
Se comparan I2 e I3 y el que tenga la aptitud mayor participa en un torneo binario con I1. El ganador de este torneo se inserta en el depósito.
Las clases formadas por BTS tienen una distribución de Boltzmann.
Aunado a esto, se inserta un párametro de temperatura para variar la presión de selección de BTS durante una corrida.
Sin embargo, nuevamente se tiene el problema de que no existe una definición formal para los cambios en la temperatura, ni de como seleccionar el valor de Q.
Se ordena la población de acuerdo al valor de aptitud de los individuos. En el progreso del AG se selecciona una constante de umbral r � \lbrack0,1]. Solo los mejores �r·N� individuos son considerados para la selección.
Se asignan probabilidades de selección iguales a los �r·N� mejores individuos. La probabilidad de selección de los N-�r·N� individuos que no son considerados en la selección se ponen igual a cero. Así,
pi = {
|
|
|